Berechnung der Höhe

Bei unserer Datenauswertung möchten wir die kosmische Strahlung sowie die Temperatur und die Luftfeuchtigkeit in Abhängigkeit der Höhe untersuchen. In den Rohdaten sind diese allerdings in Abhängigkeit der Zeit gegeben. Daher müssen wir zu jeder einzelnen Messung auch eine Höhe berechnen.

Zur Ermittlung der Höhe kann man die vom GPS-Gerät bestimmte Höhe verwenden. Diese Höhe ist in Abhängigkeit der Flugzeit in folgendem Diagramm dargestellt.
Wie man im Diagramm erkennt, gab es bei der Ermittlung der Höhe einige Aussetzer, vor allem zwischen etwa 2200 bis 5600 Sekunden nach dem Start. Die GPS-Höhe kann also nicht ohne weiteres verwendet werden, um die gemessenen Größen in Abhängigkeit der Höhe darzustellen.  

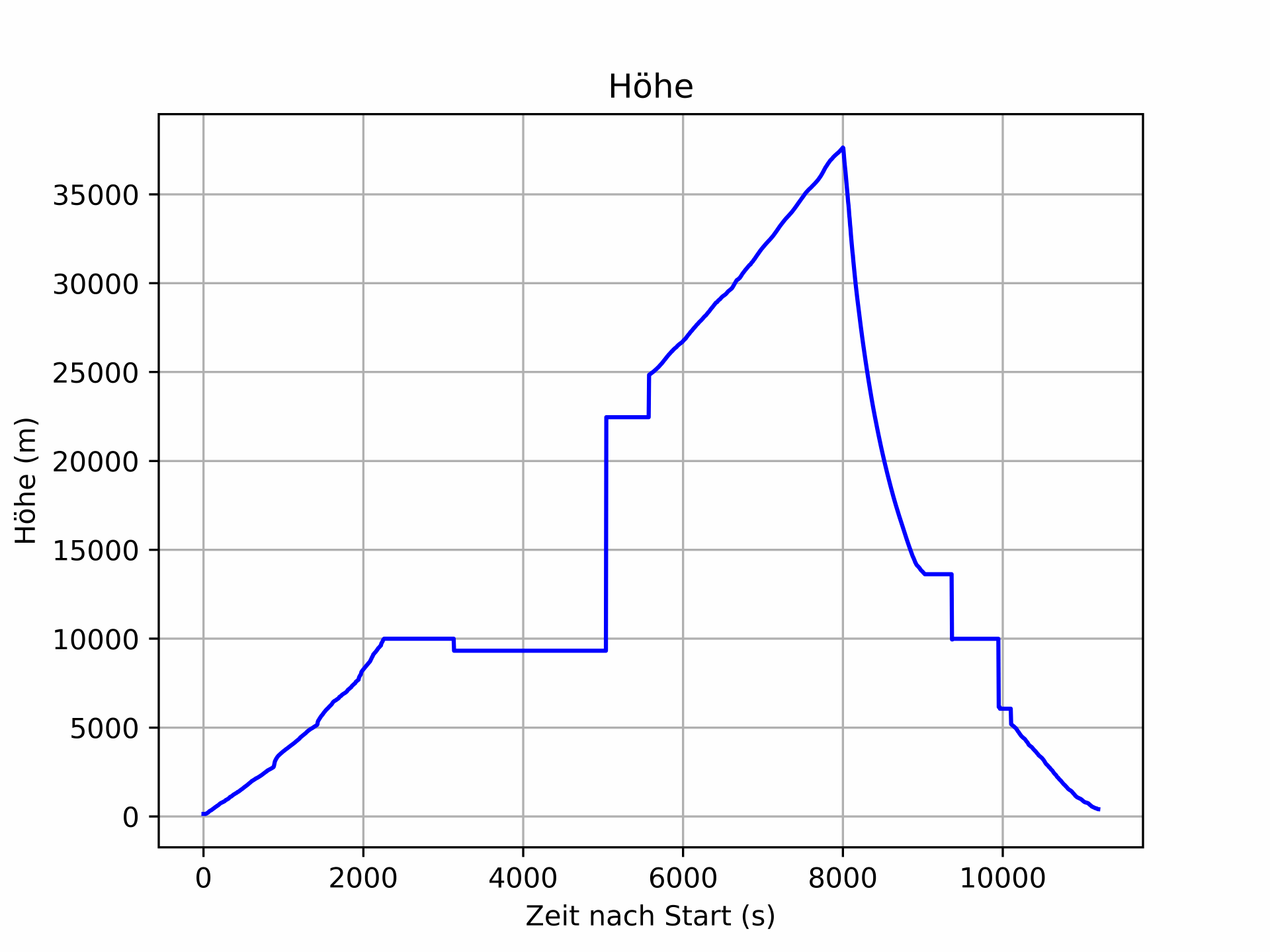
Barometrische Höhenformel

Eine andere Möglichkeit zur Ermittlung der Höhe besteht in der Berechnung durch die barometrische Höhenformel. Mithilfe der barometrischen Höhenformel lässt sich aus dem Druck die Höhe berechnen. Die einfachste Form der Formel lautet: $$ p = p_0 \cdot e^{-\frac{\rho_0}{p_0} \cdot g \cdot h} $$
Dabei ist:
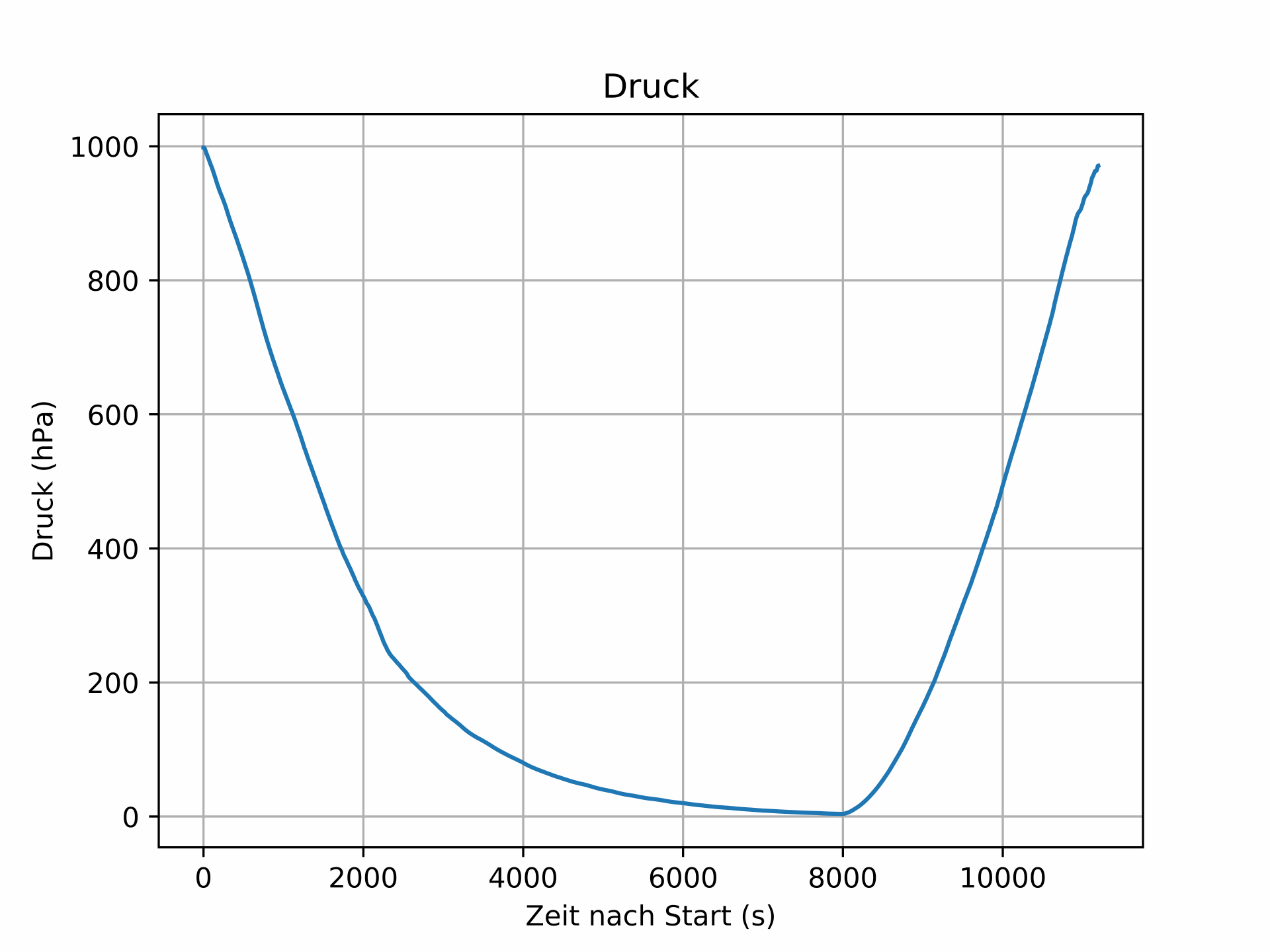
Dabei nahmen wir einen Ortsfaktor von 9,81m/s² an und gingen von der internationalen Standardatmosphäre aus, nach der der Luftdruck am Boden 1013,25 hPa beträgt [1]. Die Dichte der Luft auf Höhe des Meeresspiegels beträgt etwa 1,2041kg/m³ [2]. In dieser einfachen Form der barometrischen Höhenformel wird von einer konstanten Temperatur und einem konstanten Ortsfaktor ausgegangen. Andere Höhenformeln, die diese Veränderung berücksichtigen, stellen wir im nächsten Abschnitt vor. Stellt man obige Formel nach h um, lässt sich die Höhe aus dem Druck berechnen. Der Luftdruck ist im folgenden Diagramm dargestellt:
Zu sehen ist, dass der Luftdruck immer weiter fällt, bis er bei nur 4 hPa liegt. Nach 8000s platzt der Ballon und die Nutzlast fällt nach unten, sodass der Druck wieder schnell steigt. Die Druckkurve sieht sehr realistisch aus und hat keine Aussetzer wie die Höhe vom GPS-Gerät. Daher kann man eine gute Höhenberechnung erwarten.

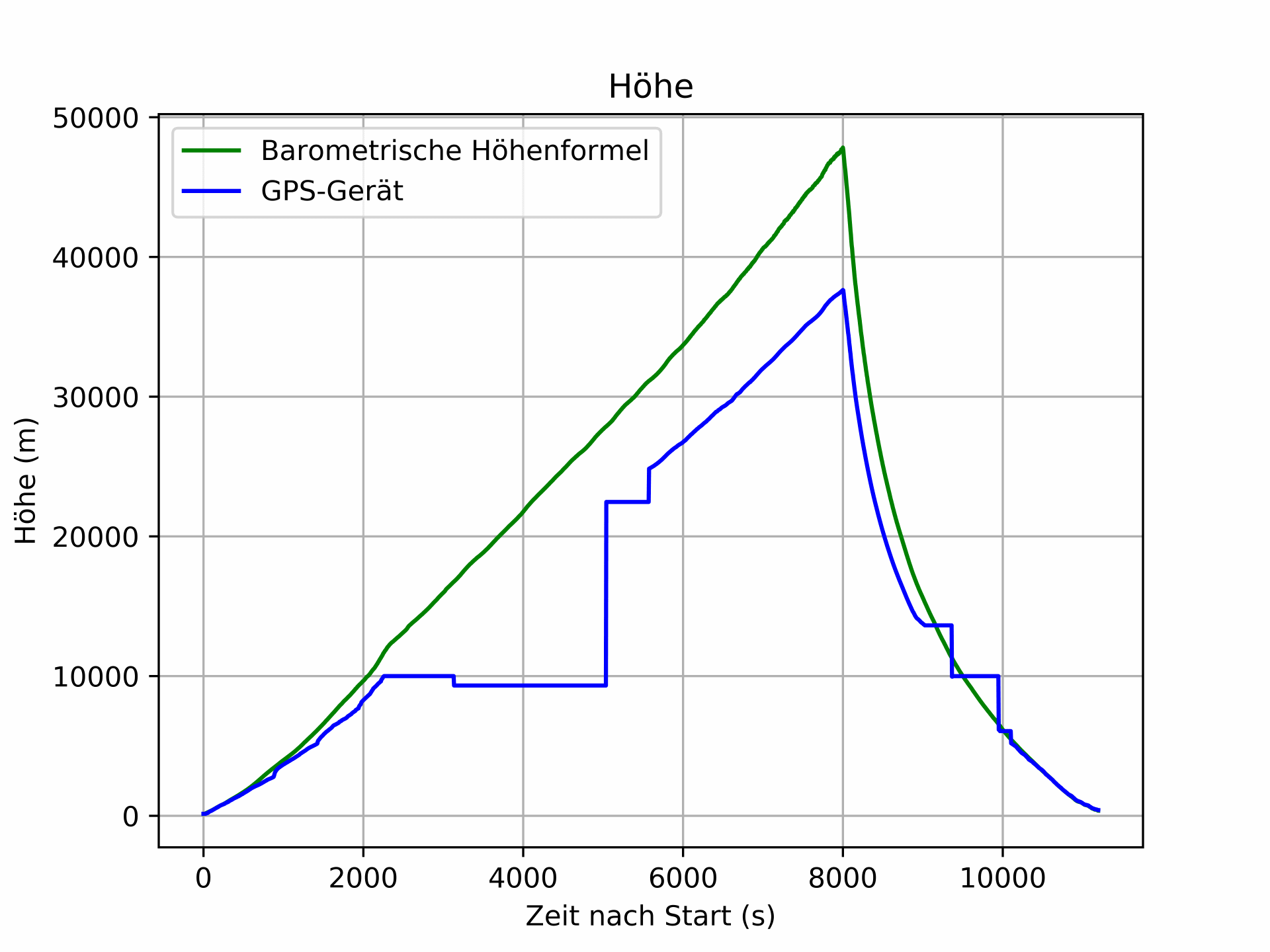
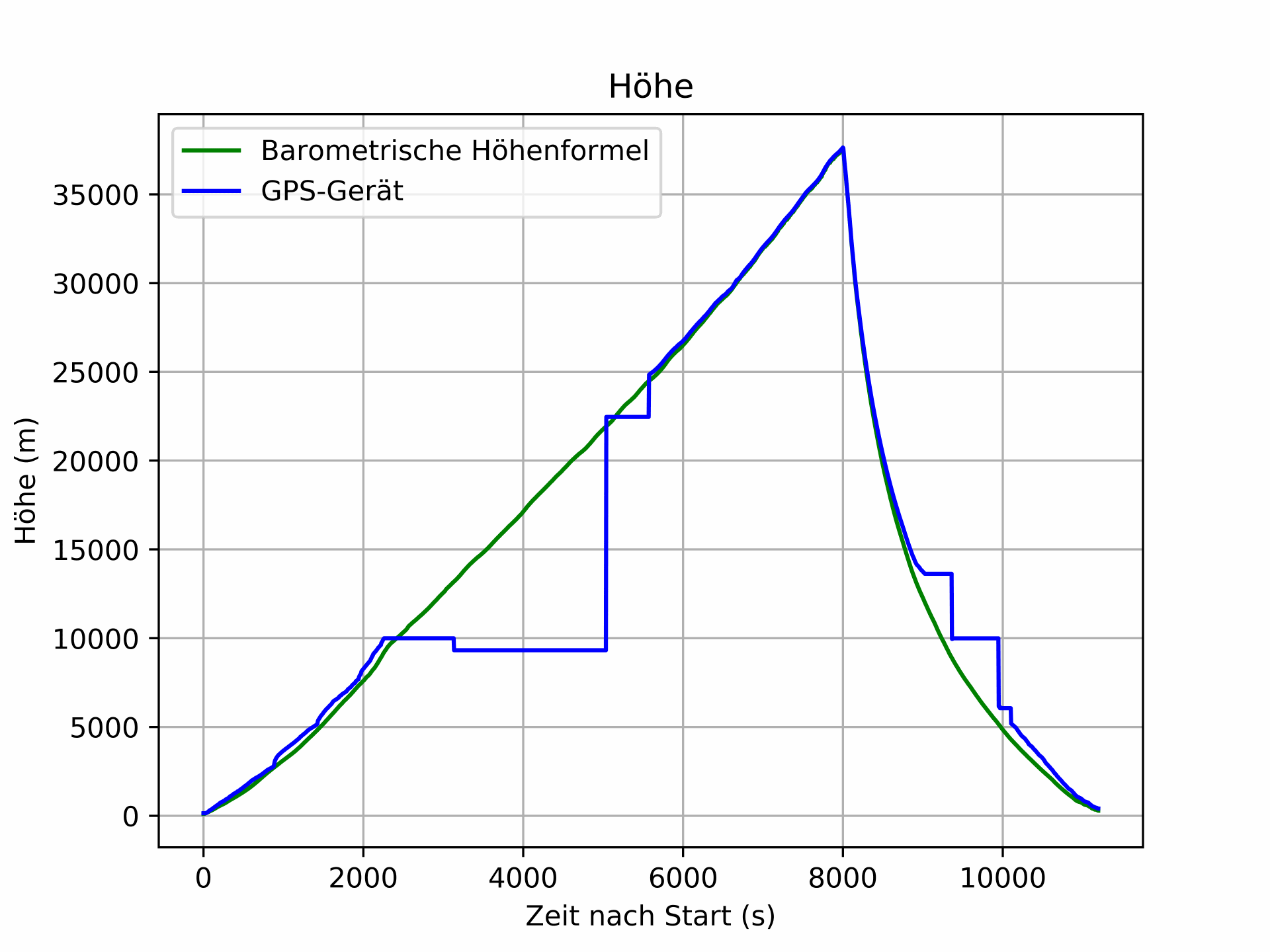
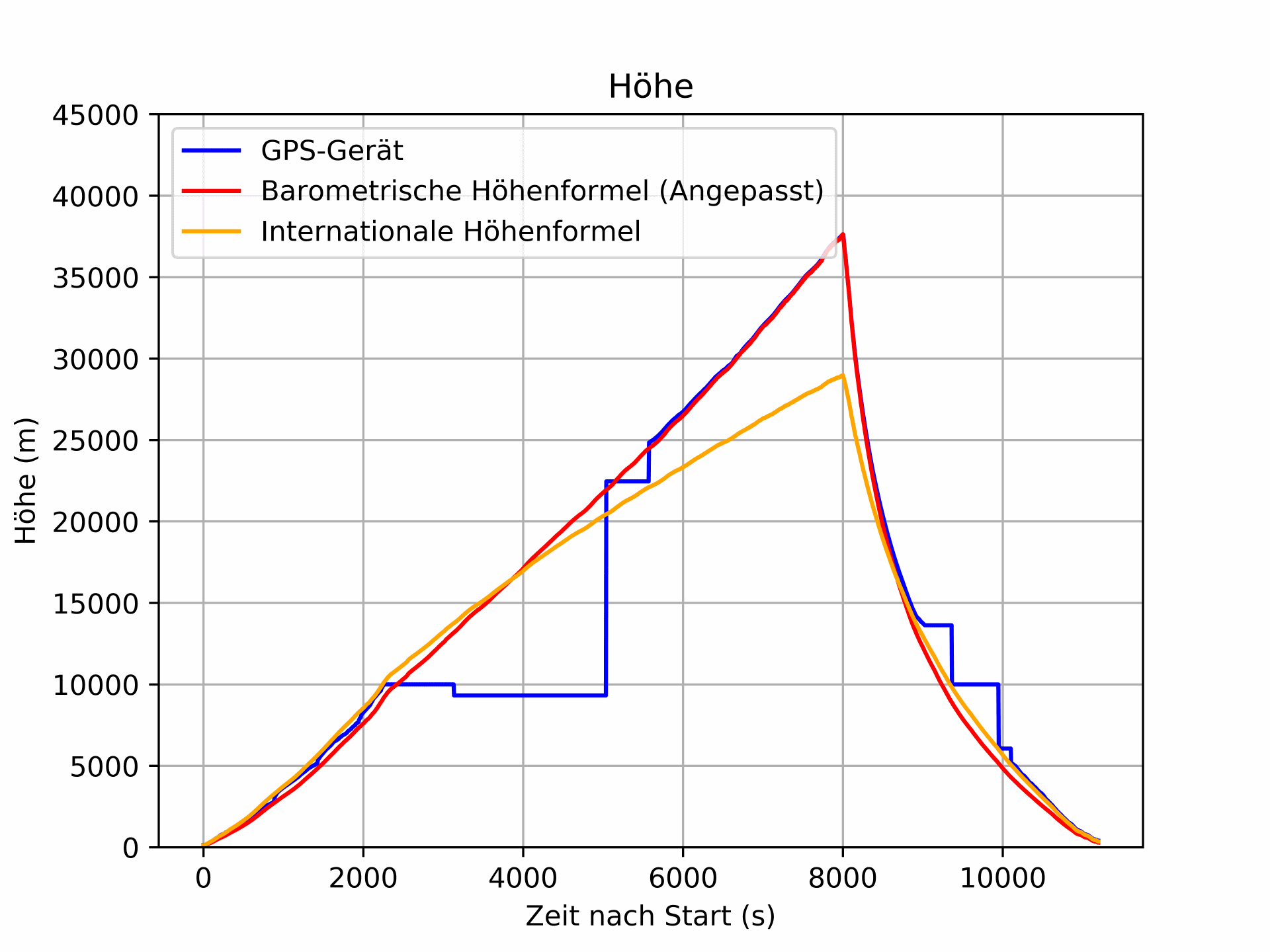
Im folgenden Diagramm ist die GPS-Höhe in blau eingezeichnet und die Höhe nach der barometrischen Höhenformel in grün.
Zu sehen ist, dass die Kurven qualitativ sehr genau übereinstimmen, die mit der barometrischen Höhenformel berechnete Höhe jedoch um etwa 27% größer ist als die GPS-Höhe. Die maximale GPS-Höhe beträgt etwa 38km und nach der barometrischen Höhenformel etwa 48km. Eine Höhe von 38km ist deutlich realistischer als 48km und bei der barometrischen Höhenformel werden einige Vereinfachungen gemacht, nämlich dass die Zusammensetzung der Luft überall gleich ist und dass die Temperatur konstant ist. Daher gehen wir davon aus, dass grundsätzlich eher die GPS-Höhe richtig ist, die Kurve nach der barometrischen Höhenformel aber besser den Verlauf beschreibt. Beide Vorteile kann man kombinieren, indem man von der Höhe nach der barometrischen Höhenformel prozentual die Abweichung abzieht. Legt man die beiden Höhenkurven dann übereinander, erhält man folgendes Diagramm.
Nun liegen beide Kurven recht gut übereinander. Diese Höhenkurve interpoliert zwischen den Aussetzern des GPS-Sensors. Mit der neu berechneten Höhe lassen sich alle Messgrößen gut in Abhängigkeit der Höhe beschreiben.

Höhenformeln mit Korrekturen

Diese einfachste Form der barometrischen Höhenformelgeht von einer konstanten Temperatur und einem konstanten Ortsfaktor aus. Es gibt auch andere Höhenformeln, die z.B. einen Temperaturgradienten berücksichtigen. Eine davon ist die Internationale Höhenformel, bei der wir uns im Folgenden auf die Formeln laut Wikipedia beziehen [3]. Wählt man dabei die Internationale Standardatmosphäre als Referenz, erhält man die Formel mit den folgenden Zahlenwerten: $$ p(h)=1013{,}25\cdot \left(1-{\frac {0{,}0065{\frac {\mathrm {K} }{\mathrm {m} }}\cdot h}{288{,}15\ \mathrm {K} }}\right)^{5{,}255}\mathrm {hPa} $$ Stellt man die Formel nach der Höhe um, folgt: $$ h={\frac {288{,}15\ \mathrm {K} }{0{,}0065{\frac {\mathrm {K} }{\mathrm {m} }}}}\cdot \left(1-\left({\frac {p(h)}{1013{,}25\,\mathrm {hPa} }}\right)^{\frac {1}{5{,}255}}\right) $$ Berechnet man nun für jede einzelne Druckmessung die Höhe, erhält man das folgende Diagramm: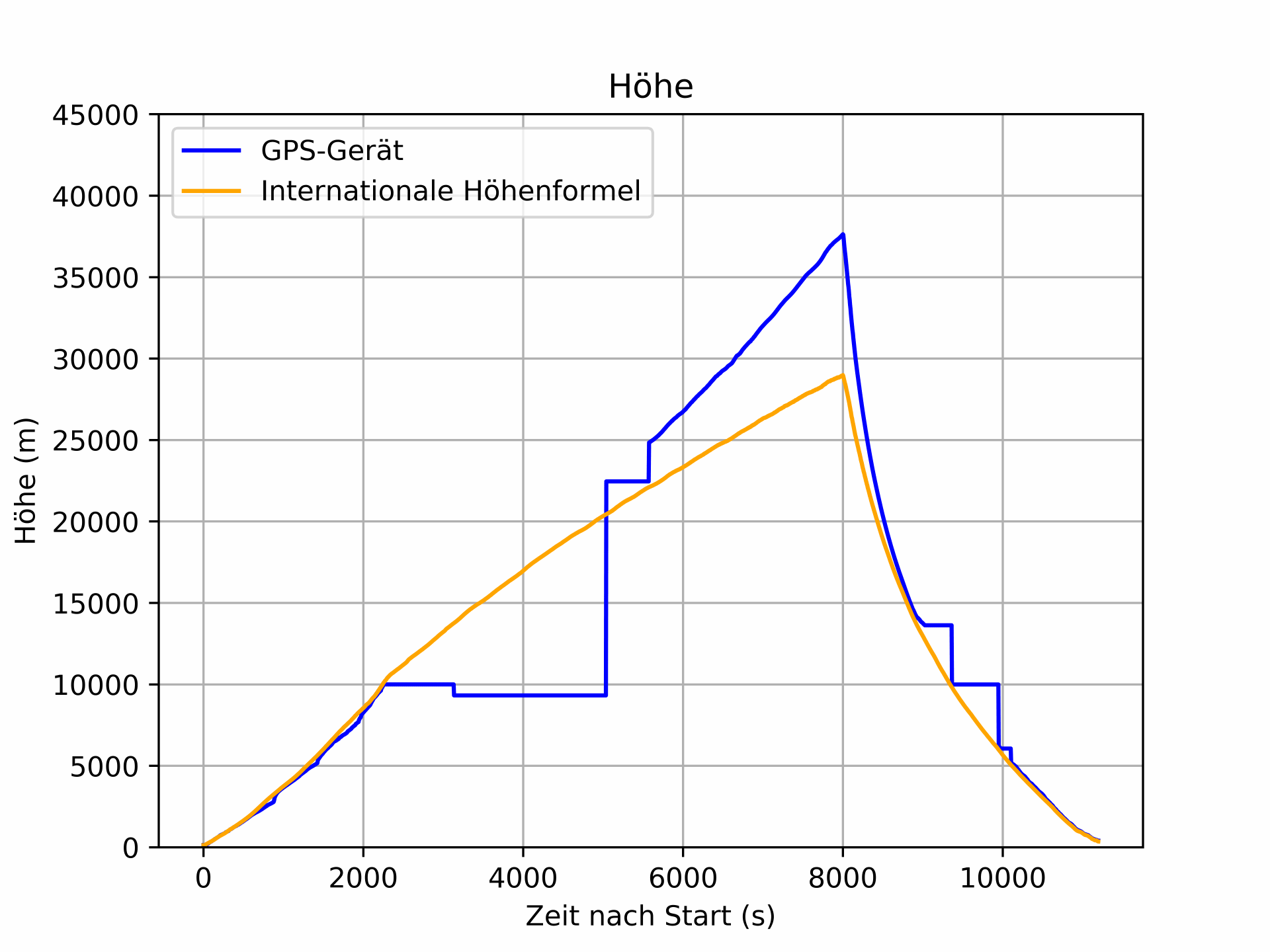
Dabei sind die mit der Formel berechneten Werte in orange eingezeichnet. Zum Vergleich ist dazu in blau die Höhe des GPS-Geräts dargestellt. Wie man dem Diagramm entnehmen kann, beschreibt die Internationale Höhenformel die Ballonhöhe unter 10-11km sehr gut. Bei größeren Höhen hingegen ist der tatsächliche Verlauf ganz anders. Dies liegt daran, dass die Internationale Höhenformel ab 11km nicht mehr gilt, da ab diesen Höhen die Temperaturgradienten deutlich anders sind. Bis zu einer Höhe von 10km nimmt die Temperatur immer weiter ab, danach steigt sie wieder an. Auch im direkten Vergleich zur einfachen Form der barometrischen Höhenformel sieht man, dass die einfache Höhenformel den Verlauf deutlich besser beschreibt.
Hierbei ist die Internationale Höhenformel wieder in orange aufgetragen und die GPS-Höhe in blau. Die rote Kurve entspricht der Höhe nach der einfachen barometrischen Höhenformel, allerdings so angepasst, dass die durch den höchsten Punkt der GPS-Höhe verläuft. Da die rote Kurve den Höhenverlauf sehr gut beschreibt und die anderen Berechnungen nicht gut im Einklang mit der Höhe nach dem GPS-Gerät stehen, haben wir uns dazu entschieden, für die folgenden Auswertungen die rote Kurve zu verwenden.

---

Quellen:
[1] Wikipedia: Normatmosphäre. In: https://de.wikipedia.org/wiki/Normatmosph%C3%A4re.
[2] Wikipedia: Luftdichte. In: https://de.wikipedia.org/wiki/Luftdichte.
[3] Wikipedia: Barometrische Höhenformel. In: https://de.wikipedia.org/wiki/Barometrische_H%C3%B6henformel#Die_H.C3.B6henstufen.